1. 题目分析

已知训练数据集D，其正实例点是$x_1 = (3, 3)$，$x_2 = (4, 3)$, 负实例点是$x_3 = (1, 1)^T$，求感知机模型

输入：训练数据集$T = \left\{(x_1, 1), (x_2, 1), (x_3, 1)\right\}$；学习率$\eta(0 < \eta \leq1)$;
输出：w, b；感知机模型$f(x) = sign(w\cdot{x} + b)$.
- 选取初值$w_0, b_0$
- 在训练集中选取数据$(x_i, y_i)$
- 如果$y_i(w\cdot{x} + b) \leq 0$
  - $w \leftarrow w + \eta{y_ix_i}$
  - $b \leftarrow b + \eta{y_i}$
- 转至(2)，直至训练集中没有误分类点

直观上的解释：当一个实例点被误分类，即位于分离超平面的错误一侧时，则调整w和b，使得分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面间的距离，直至超平面越过该误分类点使其被正确分类。

2. 算法分析

感知机完整算法请走传送门，下面将拆解分析

2.1 初始化

# 定义数据集

data = np.array([[3, 3, 1],
                 [4, 3, 1],
                 [1, 1, -1]])

rows = data.shape[0]
cols = data.shape[1]

将训练数据存储为2行3列的array，最后一列是每条数据的标签
分别得到矩阵的行数rows和列数cols，为后续遍历做准备

# 选取初值w0, b0

w = np.ones(cols - 1)
b = 0
thea = 0.001

初始化$w_0 = (1, 1)$，$b = 0$
初始化$theta$，用于图示超平面，会在下面讲解

2.2 判断条件

# 方法：判别是否存在分类错误的点

def sign(data, w, b):
    flag = False

    rows = data.shape[0]
    cols = data.shape[1]

    for row in np.arange(rows):
        x_i = data[row, :-1]
        y_i = data[row, -1]

        if y_i * (np.matmul(w, x_i.T) + b) <= 0: flag="True" break return < code>

对应算法中的第(3)步，筛选数据集中是否存在样本，使得$y_i(w\cdot{x} + b) \leq 0$成立
设置$flag$变量，若为True则存在，若为False则不存在
一旦发现不存在，马上跳出循环

2.3 图示超平面

# 方法：画散点图

def plot(data, w, b):
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.axis([0, 6, 0, 6])

    x = data[:, 0]
    y = data[:, 1]
    plt.scatter(x, y)

    x_line = [p for p in np.arange(10)]
    if w[1] == 0:
        y_line = [(-w[0]*x - b)/(w[1] + thea) for x in x_line]
    else:
        y_line = [(-w[0]*x - b)/w[1] for x in x_line]

    plt.plot(x_line, y_line)

首先，定义好坐标轴的刻度，都控制在(0, 6)之间
其次，先将数据集中的点画出来
接着，根据当前的$w, b$值，选取$x_1, x_2$
- $x_1$我们选定为(1, 10)中的整数
- 根据$w_1x_1 + w_2x_2 + b = 0$，已知$x_1$，求得$x_2$如下
  
  $x_2 = \frac{-W_1x_1 - b}{w_2}$
- 由于$w_2$可能为0，导致$x_2$求值出现问题，故我们加上一个$\theta$变量，一旦$w_2$为0，则使得$x_2$为
  
  $x_2 = \frac{-W_1x_1 - b}{w_2 + \theta}$
最后，画出超平面即可

2.4 遍历求解

# 遍历数据集

while sign(data, w, b):
    for row in np.arange(rows):
        x_i = data[row, :-1]
        y_i = data[row, -1]

        if y_i * (np.matmul(w, x_i.T) + b) <= 0: w="w" + y_i * x_i b="b" plot(data, w, b) < code>

以$sign()$函数作为条件，判断有无误分类点，一旦有就遍历循环
- 遍历每一条数据
  - 若是满足条件$y_i(w\cdot{x} + b) \leq 0$
  - 更新$w, b$
- 将当前的超平面画出

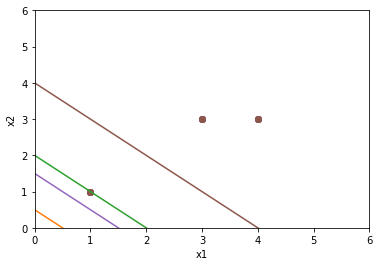
3. Sklearn实现

from sklearn.linear_model import Perceptron

# 1. 定义数据集
data = np.array([[3, 3, 1],
                 [4, 3, 1],
                 [1, 1, -1]])

# 2. 定义模型，求解
perceptron = Perceptron()
perceptron.fit(data[:, :2], data[:, 2])

# 3. 打印w,b，并图示
print("w: ", perceptron.coef_, "b: ", perceptron.intercept_)
plot(data, perceptron.coef_[0, :], perceptron.intercept_[0])

# 4. 测试模型准确率
res = perceptron.score(data[:, :2], data[:, 2])
print("correct rate:{:.0%}".format(res))